算法:第38次CCF计算机软件能力认证题目解析

September 20, 2025•by HeLong

题目1:正态分布

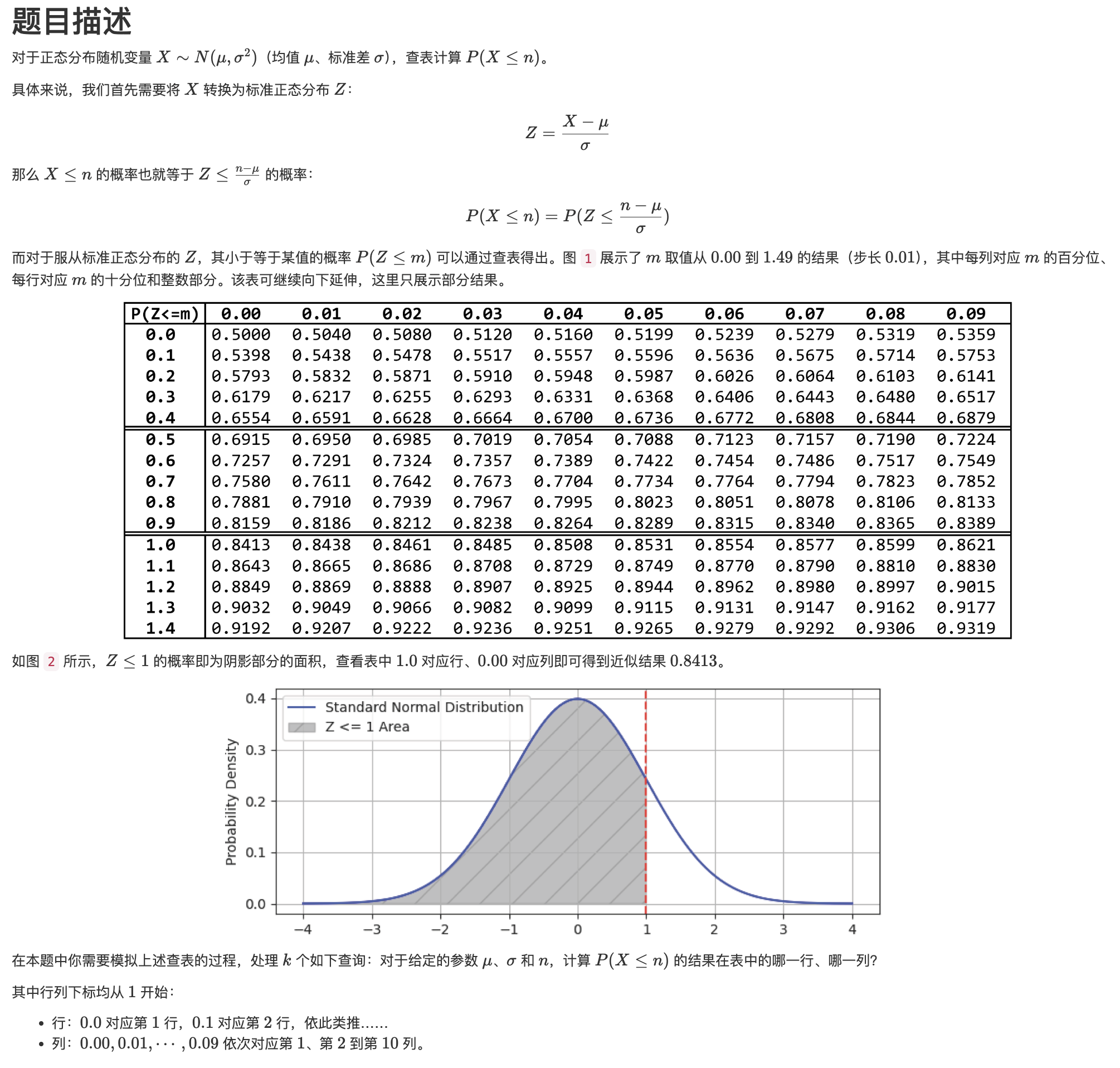
简单数学计算问题，首先将给出的 $\ P(X ≤ n)$ 转换为标准正态分布。转换公式为 $\ Z = (X - μ)/σ$ ，此时 $\ P(X ≤ n)$ 等价于 $\ P(Z ≤ m)$ ，其中 $\ m = (n - μ)/σ$ 。（均值为0、标准差为1的标准形式）。

根据计算出的标准正态分布进行查表：

行号由m值的整数部分和十分位共同决定，列号由m值的百分位决定。比如m=1.23对应的行号为1×10+2+1=13，列号为3+1=4。

代码：

python|28 lines

# main.py
import sys
data = sys.stdin.read().split()
k = int(data[0])
item = 1
results = []
for _ in range k:
	miu = int(data[item + 1])
	sig = int(data[item + 2])
	n = int(data[item +3])

	item = item + 3

	m = (n - miu)/sig
	# 小数部分
	xiaoshu = m - int(m)
	# 十分位和百分位
	tenths = int(xiaoshu * 10 + 1e-9)
    hundredths = int((xiaoshu * 100 - tenths * 10) + 1e-9)
	# 计算行和列
	row = int(m) + tenths * 0.1

	col = hundredths * 0.01

	results.append(f"{row} {col}")

for res in results:
    print(res)

题目2:机器人复健指南

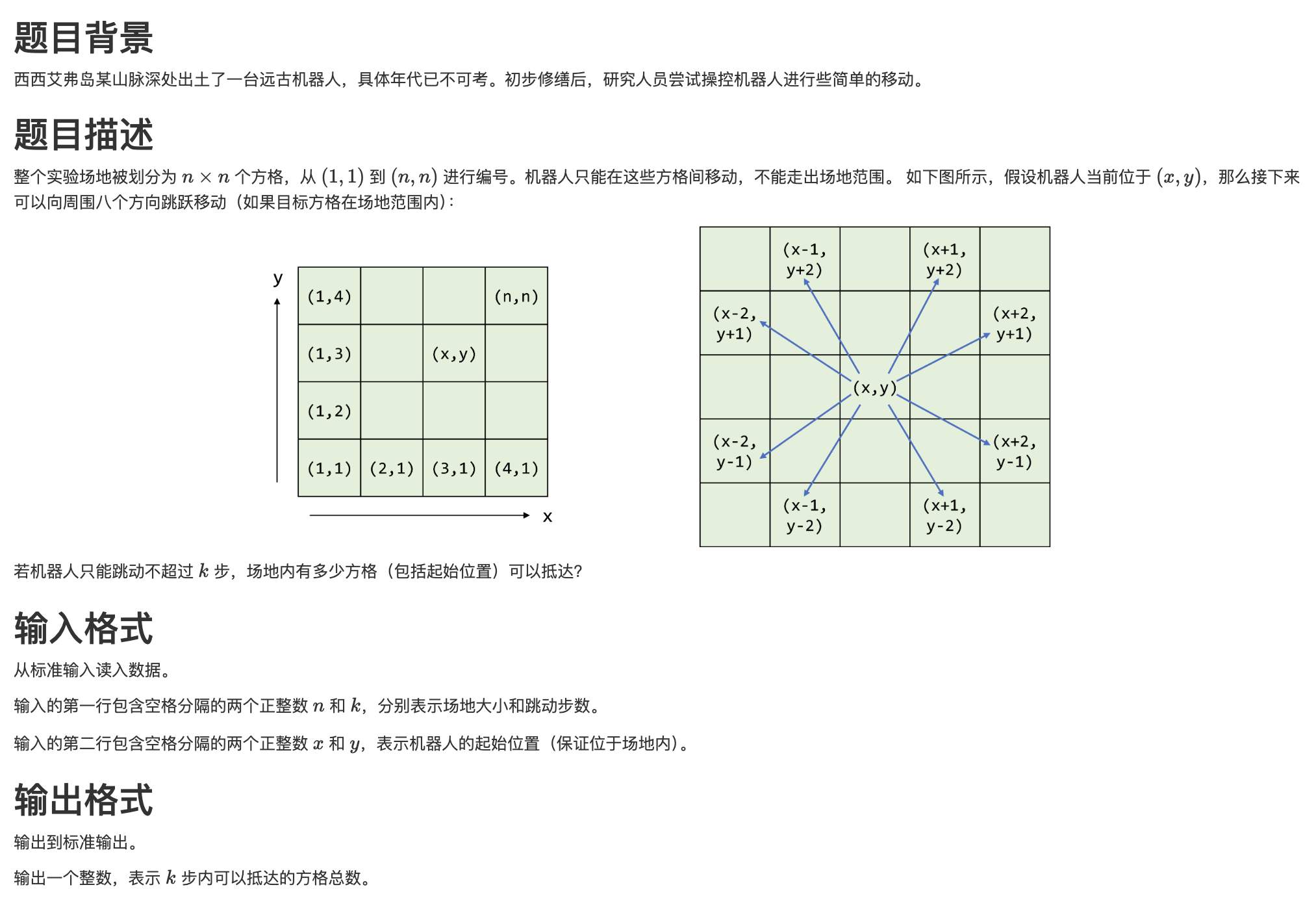
典型的图遍历问题，要求计算在n×n的棋盘上，机器人从起始位置出发，在k步内能够到达的所有不同方格数量。采用广度优先搜索（BFS）算法，注意处理重复和边界即可。

Breadth-first search

Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property.

代码：

python|49 lines

# main.py
from collections import deque

# 定义8个方向的移动向量
px = [1, 2, 2, 1, -1, -2, -2, -1]  # x方向移动
py = [2, 1, -1, -2, -2, -1, 1, 2]  # y方向移动

def main():
    n, k = map(int, input().split())
    x, y = map(int, input().split())

    # 初始化访问标记矩阵和队列
    st = [[False] * (n + 1) for _ in range(n + 1)]
    q = deque()

    # 标记起始位置并加入队列
    st[x][y] = True
    q.append(((x, y), k))
    ans = 1  # 起始位置已经访问

    while q:
        (nx, ny), nk = q.popleft()  # 当前位置和剩余步数

        # 尝试8个方向的移动
        for i in range(8):
            tx = nx + px[i]  # 目标x坐标
            ty = ny + py[i]  # 目标y坐标
            tk = nk - 1      # 剩余步数减1

            # 检查是否越界
            if tx < 1 or ty < 1 or tx > n or ty > n:
                continue

            # 检查是否已访问
            if st[tx][ty]:
                continue

            # 标记为已访问，增加计数
            st[tx][ty] = True
            ans += 1

            # 如果还有剩余步数，加入队列继续搜索
            if tk != 0:
                q.append(((tx, ty), tk))

    print(ans)

if __name__ == "__main__":
    main()

题目3:消息解码

题目

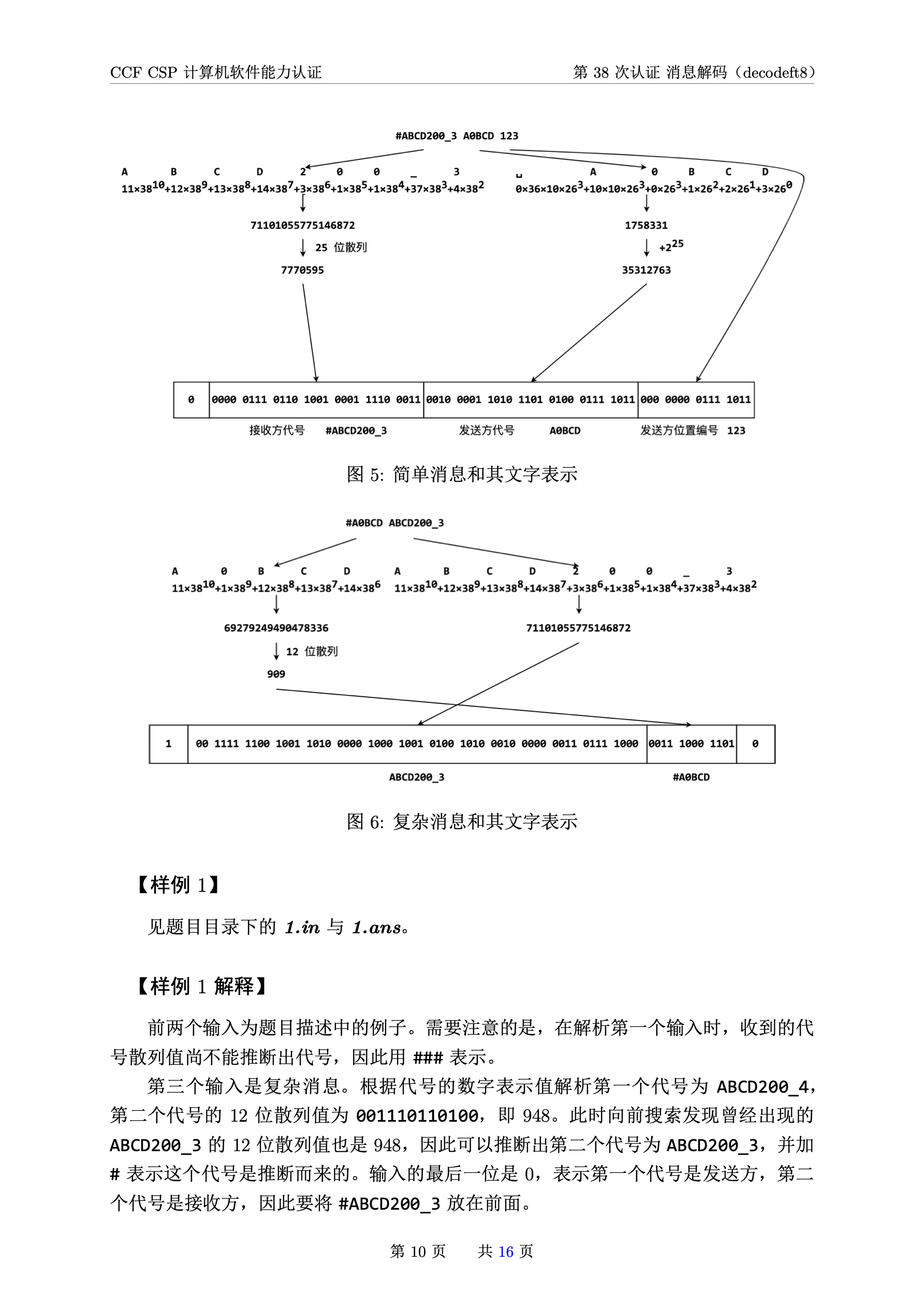
解析

等待更新～～

算法:第38次CCF计算机软件能力认证题目解析

题目1:正态分布

题目2:机器人复健指南

题目3:消息解码

题目

解析

Comments